

This guide documents CULA Sparse’s programming interface. CULA Sparse™ is an implementation of sparse linear algebra routines for multi-core CPUs and CUDA-enabled NVIDIA graphics processing units (GPUs). This guide is split into the following sections:
- Using the API - A high level overview of how to use configure, use, and interpret the results from the iterative solvers in the CULA Sparse library.
- Type Definitions - A description of the all data types used the library.
- Platforms - An overview of the computation platforms available in the library.
- Data Formats - An overview of the data formats avaialable in the library.
- Iterative Preconditioners - An overview of the preconditioners available in the library.
- Iterative Solvers - A description of the iterative solvers functions available in the library.
- Auxiliary Routines - A description of the auxiliary functions available in the library.
- Performance and Accuracy - Information on how to maximize the performance of the library. Also includes a handful of performance charts.
- Common Errors - Solutions to errors commonly encountered when using the API.
Many problems in science and engineering, particularly those related to partial differential equations (PDEs), can be represented by a linear system where only a few elements in the matrix are non-zero. For these systems, it would be wasteful, in both storage and computation, to represent all of the elements. To address these common problems, storage formats and methods have been developed to solve sparse matrices with minimal memory and computation requirements. These methods can be broken into two main categories: direct methods and iterative methods.
Direct methods, common for dense matrices, attempt to solve system in a two-step process. Typical algorithms include LU and QR factorization where the linear system is transformed into an equivalent system that can be solved using Gaussian elimination. Direct methods can also be applied to sparse systems but algorithms become increasingly complex in an attempt to minimize storage and computation.
The other class of sparse solvers, and those currently implemented in CULA Sparse, are iterative methods. These methods attempt to coverage on solution to the system \(Ax=b\) by continuously iterating over new solutions until a solution’s residual, typically defined as \(||b-Ax||/||b||\), is under a given tolerance. At each step, a solution is calculated using a technique specific to the given algorithm. Because it is possible for iterative methods to fail to find a solution, they are commonly configured with a maximum number of iterations.
A common method to improve the speed at which a solution converges is called preconditioning. These methods attempt, at each iteration, to transform the original linear system into a new equivalent system that can more readily be solved. This adds overhead, in both memory and time per iteration, but will often result in a shorter end-to-end solution time.
CULA Sparse intends to support the full range of operating systems that are supported by CUDA. Installers are currently available for Windows, Linux, and MAC OS X in 32-bit and 64-bit versions. CULA Sparse has been tested on the following systems:
Please provide feedback on any other systems on which you attempt to use CULA Sparse. Although we are continually testing CULA Sparse on other systems, at present we officially support the above list. If your system is not listed, please let us know through the provided feedback channels.
This work has been made possible by the NASA Small Business Innovation Research (SBIR) program. We recognize NVIDIA for their support.
CULA Sparse is built on NVIDIA CUDA and NVIDIA CUSPARSE.
CULA Sparse uses COLAMD, covered by the GNU LGPL license. The source code for COLAMD is used in an unmodified fashion; a copy of this code is distributed in the src/suitesparse directory of this package.
CULA Sparse uses Thrust, released in the CUDA toolkit and covered by the Apache 2.0 license. The Thrust code is used in unmodified form and is covered by the license at http://www.apache.org/licenses/LICENSE-2.0.html
Many of the algorithms and methods from this library were developed based on Yousef Saad’s textbook “Iterative Methods for Sparse Linear Systems”.
CULA Sparse uses the Intel® Math Kernel Library (MKL) internally. For more information, please see the MKL product page at http://www.intel.com/software/products/mkl
While not required, CULA Sparse can optionally utilize CUDA-enabled GPUs to perform accelerated linear algebra operations. To use these functions an NVIDIA GPU with CUDA support is required. A list of supported GPUs can be found on NVIDIA’s CUDA Enabled webpage.
Support for CUDA accelerated double-precision operations requires a GPU that supports CUDA Compute Model 1.3. To find out what Compute Model your GPU supports, please refer to the NVIDIA CUDA Programming Guide.
Installation is completed via the downloadable installation packages. To install CULA Sparse, refer to the section below that applies to your system.
Windows
Run the CULA Sparse installer and when prompted select the location to which to install. The default install location is c:\Program Files\CULA\S#, where S# represents the release number of CULA Sparse.
Linux
It is recommended that you run the CULA Sparse installer as an administrator in order to install to a system-level directory. The default install location is /usr/local/culasparse.
Mac OS X Leopard
Open the CULA Sparse .dmg file and run the installer located inside. The default install location is /usr/local/culasparse.
Note
You may wish to set up environment variables to common CULA Sparse locations. More details are available in the Configuring Your Environment chapter.
CULA Sparse presents two main C headers, cula_sparse.h and cula_sparse_legacy.h. You must include one of these headers in your C source file to use CULA Sparse. These main headers rely on three supplemental headers, cula_sparse_common.h, cula_sparse_options.h, and cula_sparse_defs.h. These files are included automatically by the main C headers and shouldn’t typically be included directly by users.
CULA Sparse provides a link-time stub library, but is otherwise built as a shared library. Applications should link against the following libraries:
Windows
Choose to link against cula_sparse.lib as a link-time option.
Linux / Mac OS X Leopard
Add -l -lcula_sparse to your program’s link line.
CULA Sparse is built as a shared library, and as such it must be visible to your runtime system. This requires that the shared library is located in a directory that is a member of your system’s runtime library path. For more detailed information regarding operating-system-specific linking procedures, please refer to the Configuring Your Environment chapter.
The CULA Sparse’s example projects are a good resource for learning how to set up CULA Sparse for your own project.
Note
CULA Sparse is built against NVIDIA CUDA 5.0 and ships with a copy of the CUDA 5.0 redistributable files. If you have a different version of CUDA installed, you must ensure that the CUDA runtime libraries shipped with CULA Sparse are the first visible copies to your CULA Sparse program. This can be accomplished by placing the CULA Sparse bin path earlier in your system PATH than any CUDA bin path. If a non-CUDA 5.0 runtime loads first, you will experience CULA Sparse errors.
CULA Sparse is also built against Intel OpenMP 5 and ships with a copy of the Intel OpenMP 5 runtime redistributable file.
After installation, CULA Sparse leaves a record to uninstall itself easily. To uninstall CULA Sparse, refer to the section below that applies to your system.
Windows
From the Start Menu, navigate to the CULA Sparse menu entry under Programs, and select the Uninstall option. The CULA Sparse uninstaller will remove CULA Sparse from your system.
Linux
Run the CULA Sparse installer, providing an ‘uninstall’ argument.
e.g. ./cula.run uninstall
Mac OS X Leopard
There is no uninstallation on OS X, but you can remove the folder to which you installed CULA Sparse for a complete uninstall.
Note
If you have created environment variables with references to CULA Sparse, you may wish to remove them after uninstallation.
This chapter describes, at a high level, how to use the CULA Sparse API. Basic information about how to initialize and configure an iterative solver is discussed. Furthermore, we introduce how to collect and interpret the results from the iterative solvers as well any error condition that may occur.
Further specifics are found in the subsequent chapters.
To convey the status of a given function call, all CULA Sparse functions return a culaSparseStatus code.
The culaSparseStatus return code is unique to the CULA Sparse library. It is a high level status code used to indicate if the associated call has completed successfully. It conveys non-specific information such as:
- Success condition
- Non-convergence condition
- Parameter errors
- GPU runtime errors
- Out of memory errors
Additional information regarding the last status code may be obtain by examining the string returned by culaSparseGetLastStatusString. This routine will return a string with in-depth information regarding the actual error. For example, on an argument error it will report which parameter is in error and why.
The CULA Sparse library is initialized by calling the culaSparseCreate() function to create a library handle. This handle provides serialized thread-safe access and is used as input to all CULA Sparse library functions. When using CULA Sparse on multiple host threads, it is recommended to create a handle for each thread.
#include <cula_sparse.h>
// create library handle
culaSparseHandle handle;
culaSparseStatus status = culaSparseCreate(&handle);
// run library functions
// ...
// clean up library handle
culaSparseDestroy(handle);
The CULA Sparse library offers two main interfaces:
Prior to CULA Sparse version S5, the legacy interface was the only interface available and was named cula_sparse.h. However, this was succeeded by the plan interface found in the current version of cula_sparse.h. The plan interface offers a vastly reduced number of functions, improved performance, and better control compared to the legacy interfaces. The old-style interface is still available in the cula_sparse.h header.
The general usage pattern of the plan interface requires the user to create a “plan” object which is then associated with a platform, data format, solver method, and preconditioning strategy. One all options have been set, the plan is executed with the specified settings. The plan interface offers the benefit that data is cached within the plan. For example, if a plan with the ilu0 preconditioner is executed with the gmres solver, changing the plan to be associated with the bicgstab solver will not require the ilu0 preconditioner to be regenerated.
In the legacy interface, all state is encapsulated within a single function call. While this is fundamentally simple to use, the increased flexibility of the plan interface is lost.
When using the standard CULA Sparse interface, users must create a plan to describe the platform, preconditioner, and solver to be used. Multiple plans may be associated with one library handle.
#include <cula_sparse.h>
// create plan
culaSparseStatus status = culaSparseCreatePlan(handle, &plan);
// set up and execute plan
// ...
// clean up plan
status = culaSparseDestroyPlan(plan);
The first step of using a plan is to associate with an execution platform.
In CULA Sparse, the Host and Cuda platform (e.g. culaSparseSetHostPlatform() and culaSparseSetCudaPlatform()) will interpret pointers to matrices and vectors as data allocated on the host; that is, data allocated with malloc(), new, or std::vector. For the Cuda platform, CULA Sparse will automatically transfer the data to-and-from the accelerated device. This step is performed concurrently to other operations and in non-trivially small problems yields almost no performance impact for this transfer.
Alternatively, the CudaDevice platform (e.g. culaSparseSetPlatform()) only accept pointers to matrix and vector data allocated on a CUDA GPU; that is, data allocated with cudaMalloc(). When using this data interfaces, be sure that the deviceId field in the :c:func`culaSparseCudaDeviceOptions` options structure matches the CUDA device where allocation has occurred. This data interface is typically used when a sparse matrix has been assembled previously on the GPU. It is not recommended that users manager their own data in an attempt to gain performance.
// allocate solver data on host using malloc (C)
double* data = (double*) malloc(nnz * sizeof(double));
// allocate solver data on host using new[]
double* data = new double[nnz];
// allocate solver data on host using a std vector (C++)
std::vector<double> data(nnz);
// allocate solver data on a CUDA device using cudaMalloc
double* data;
cudaError_t status = cudaMalloc(&data, nnz * sizeof(double));
CULA Sparse currently supports three major matrix storage formats: coordinate, compressed row, and compressed column. It is recommended to use the compressed row format when possible as internally, all input formats are converted to this format.
In the coordinate format, a sparse matrix is represented by three vectors sized by the number of non-zero elements of the system. The common abbreviation for this length, \(nnz\) is used throughout the API and this document. In CULA Sparse, these vectors do not need to be sorted in any fashion, though higher performance is possible if they are sorted by row indices.
- values - the non-zero data values within the matrix; length \(nnz\)
- row index - the associated row index of each non-zero element; length \(nnz\)
- column index - the associated column index of each non-zero element; length \(nnz\)
Consider the following 3x3 matrix with 6 non-zero elements:
In a zero-indexed coordinate format, this matrix can be represented by the three vectors:
In the CULA Sparse interface, the values are denoted as a, the column index as colInd, and the row index as rowInd.
In the compressed sparse row format, the row index vector is replaced by a row pointer vector of size \(m+1\). This vector now stores the locations of values that start a row; the last entry of this vector points to one past the final data element. The column index is as in COO format.
Consider the same 3x3 matrix, a zero-indexed CSR format can be represented by three vectors:
In the CULA Sparse interface, the values are denoted as a, the column index as colInd, and the row pointer as rowPtr.
In the compressed sparse column format, the column index vector is replaced by a column pointer vector of size \(n+1\). This vector now stores the locations of values that start a column; the last entry of this vector points to one past the final data element. The row index is as in COO format. In CULA Sparse, the row indices must be sorted on a per-column basis.
Consider the same 3x3 matrix, a zero-indexed CSC format can be represented by three vectors:
In the CULA Sparse interface, the values are denoted as \(a\), the column pointer as colPtr, and the row index as rowInd.
In the matrix free format, the user provides a pointer to function that performs \(x' = A*x\) instead of explicitly calculating the value. This gives support for a number of exotic matrix storage formats. When using this format, only user definied preconditioners are available.
CULA Sparse supports both 0 (C/C++) and 1 (Fortran) based indexing through the indexing field of the data format configuration structures. The default is zero-based indexing.
#include <cula_sparse.h>
// initialize format options
culaSparseCooOptions formatOpts;
culaSparseCooOptionsInit(handle, &formatOpts)
// change the indexing on host data to 1-based (Fortran style)
formatOpts.indexing = 1;
CULA Sparse provides four data types with which you can perform computations.
| Symbol | Interface Type | Meaning |
|---|---|---|
| S | float | single precision real floating point |
| D | double | double precision real floating point |
| C | culaSparseComplexFloat | single precision complex floating point |
| Z | culaSparseComplexDouble | double precision complex floating point |
Note
Many sparse linear systems will require double precision arithmetic to converge on an acceptable answer.
The complex types provided by CULA Sparse are simple structs containing real and imaginary floating point elements. Additional steps are taken to insure the values are 16-byte aligned as required by many vector processing units.
It is possible to utilize C99 complex values for the Host and Cuda platforms or NVIDIA’s cuComplex when using the CudaDevice platform. The pointers will simply need to be cast to the appropriate culaSparseCompelxFloat or culaSparseComplexDouble type when passed in the CULA Sparse API.
Using the plan interface, the data format and numeric type are chosen using the culaSparseSet{format}{storage}Data(...) routines.
Example selection:
#include <cula_sparse.h>
// initialize format options
culaSparseCooOptions formatOpts;
culaSparseCooOptionsInit(handle, &formatOpts)
// associate double precession compressed sparse row data with a plan
status = culaSparseSetDcsrData(handle, plan, &platformOpts, n, nnz, a, rowPtr, colInd, x, b);
Note
When interacting with platforms, both the Host and Cuda platforms use pointers to memory allocated on the CPU while the CudaDevice platform uses memory previously allocated by CUDA.
For more information regarding these storage formats, we recommend reading Section 3.4, Storage Schemes, Yousef Saad’s textbook “Iterative Methods for Sparse Linear Systems”.
All execution routines within CULA Sparse utilize a common configuration parameter to steer the execution of the solver. The configuration parameter is represented by the culaSparseConfig structure and is the first parameter to any solver function within the library. The configuration parameter informs the API of the desired solve by specifying:
- The relative tolerance at which a solve is considered as converged (relative to r0)
- The absolution tolerance at which solve is considered as converged
- The divergent tolerance at which solve is considered as diverged (relative to r0)
- The maximum number of iterations to attempt
- The maximum time to execute the solve
- Per-iterative result vector
More parameters may be added in the future.
Configuration parameters must be set up before a solver can be called. The configuration parameter is initialized by the culaSparseConfigInit() function. This function ensures that all parameters within this structure are set to reasonable defaults. After calling this function, you may set specific parameters to your needs.
Example configuration:
#include <cula_sparse.h>
// create configuration structure
culSparseConfig config;
// initialize values
culaIterativeConfigInit(&config);
// configure specific parameters
config.relativeTolerance = 1e-6;
config.maxIterations = 300;
config.maxRuntime = 10;
Choosing a proper solver is typically determined by the class of the input data. For example, the CG method is only appropriate for symmetric positive definite matrices.
Using the plan interface, a solver is chosen the culaSparseSet{name}Solver() routines.
Example solver selection:
#include <cula_sparse.h>
// create default cg options
culaSparseCgOptions solverOpts;
culaSparseStatus status = culaSparseCgOptionsInit(handle, solverOpts);
// associate cg solver with the plan
status = culaSparseSetCgSolver(handle, plan, &solverOpts);
As a general note, for any routine that takes an option or configuration parameter a null value (e.g. 0 or null_ptr) will result in default options being selected.
Preconditioner selection is more of an art - the method chosen is tightly coupled to the specifics of the linear system. That is, the computational tradeoffs of generation and application of the preconditioner will be different for different systems.
Using the plan interface, a preconditioner is chosen the culaSparseSet{name}Preconditioner() routines.
For example:
#include <cula_sparse.h>
// create default ilu0 options
culaSparsesIlu0Options precondOpts;
culaSparseStatus status = culaSparseIlu0OptionsInit(handle, precondOpts);
// associate ilu0 solver with the plan
status = culaSparseSetIlu0Preconditioner(handle, plan, &precondOpts);
Once a plan has been assembled, it can be executed using the culaSparseExecutePlan() routine. Note that no computation, other than parameter checking, is performed until the plan is executed. This routine is responsible for the actual data management, preconditioner generation, and the iterative solve.
For example:
#include <cula_sparse.h>
// information returned by the solver
culaSparseResults results;
// execute the plan
culaSparseStatus status = culaSparseExecutePlan(handle, plan, &config, &results);
The plan data structure allows for some advanced usage that some users might useful:
- A plan may be executed multiple times
- Executing a plan with no data platform set will result in a culaSparseNoError status and a flag indicating culaSparseSolveNotExecuted
- Executing a plan with just the data platform cache the data preparation
- Executing a plan with just the data platform and the preconditioner will cache the data preparation the precondtioner generation
- Options may be out of scope when the plan is executed
- Input data must be in scope when the plan is executed
- If the input data changes after plan execution, the plan cache should be cleared by calling culaSparseClearPlanCache()
The culaSparseResult structure provides additional information regarding the computation such as:
- A flag that denotes why the solver converged, diverged, or failed to converge
- The number of iterations performed, regardless of whether this led to convergence
- The solution residual when the solve ended
- Timing information for the overhead, preconditioner generation, and solving
This structure is returned by the culaSparseExecutePlan routine.
CULA Sparse also provides a utility function for culaSparseResult, which is called culaSparseGetResultString(), that constructs a readable string of information that is suitable for printing. In many cases, this function is able to provide information beyond that which is available by inspection of the structure, and so it is recommended that it be used whenever attempting to debug a solver problem.
// allocate result string buffer
const int bufferSize = 256;
char buffer[bufferSize];
// fill buffer with result string
culaIterativeResultString( handle, &result, buffer, bufferSize );
// print result string to screen
printf( "%s\n", buffer );
Example output:
storage: compressed sparse row (cuda)
preconditioner: factorized approximate inverse
solver: cg
result flag: the maximum runtime was exceeded
iterations: 1673
relative residual: 2.17918
absolute residual: 2637.75
overhead time: 0.00666568 s
precond. time: 1.268 s
solver time: 20.0115 s
total time: 21.2862 s
In CULA Sparse, the culaSparseNonConvergence return status is used to describe any condition for which the solver executed, but failed to converge on solution within the given configuration parameters.
Possible reasons for returning a culaSparseNonConvergence include:
- Maximum number of iterations exceeded without reaching desired tolerance
- An internal scalar quantity became too large or small to continue
- The method stagnated
- Maximum runtime was
These possible reasons are enumerated by the flag field of the culaSparseFlag structure.
In some cases, a user may wish to get the best possible result in a fixed number of iterations. In such a case, a status can be interpreted as success if and only if the flag is culaSparseMaxIterationsReached. The residual should then be consulted to judge the quality of solution obtained in the budgeted number of iterations.
For convenience, the culaSparseResult result structure contains high precision timing information regarding the runtime of the iterative solver. This timing is broken down into three major components:
- Overhead - This includes memory allocations, transfers to-and-from the GPU, and internal operations such as storage type conversion.
- Preconditioner - The time taken to generate the requested preconditioner. This does not include the per-iteration time to apply the preconditioner; the per-iteration time of a preconditioner is included in the solver time.
- Solver - This represents the time spent in the actual iteration loop
Additionally, the total time is returned which is a sum of these three values. All values are in seconds.
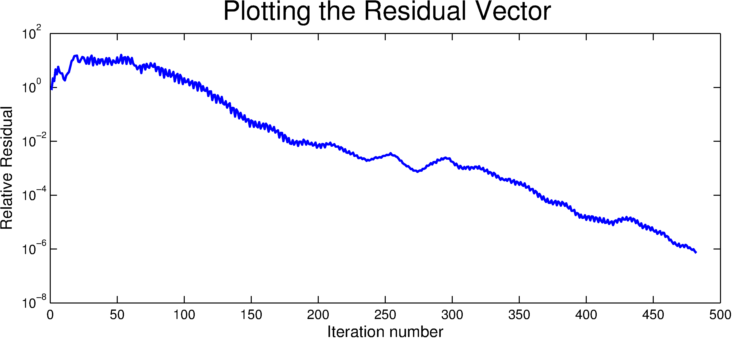
For some users, it may be desirable to capture the relative residual of the solver at each iteration. CULA Sparse provides a mechanism to obtain this information, via a parameter in the configuration structure. This parameter, result.byIteration is normally set to NULL, but may be assigned by the user to specify an array into which the residual by iteration should be stored. It is up to the user to ensure that this location has enough memory to store the residual for each iteration; in practice this is achieved by ensuring that the specified array is long enough to store one double precision value for each requested iteration.
This function describes the various data types defined in the CULA Sparse library. These types are accepted as arguments by or returned by various interface functions in the library, which will be described later.
The data types are declared in the cula_sparse_defs.h header.
The culaSparseStatus type is used for all status returns. All CULA Sparse functions return their statuses with the following values being defined:
| Status Code | Meaning |
|---|---|
| culaSparseNoError | The command completed successfully |
| culaSparseNonConvergence | The iterative solver did not converge within the selected constraints |
| culaSparsePreconditionerError | The selected preconditioner failed to generate |
| culaSparseArgumentError | An invalid argument was passed to a function |
| culaSparseDataFormatError | The matrix data format is malformed |
| culaSparseInsufficientMemory | There is insufficient memory to continue |
| culaSparseFeatureNotImplemented | The requested feature has not been implemented |
| culaSparseRuntimeError | A runtime error has occurred |
| culaSparseAlignmentError | Unaligned data was encountered when required |
| culaSparseInteralError | An internal error has occurred |
| culaSparseHandleError | An invalid reference handle was passed to a function |
| culaSparsePlanError | An invalid execution plan was passed to a function |
| culaSparseUnspecifiedError | An unspecified internal error has occurred |
For more information about various failure status conditions, see the Common Errors chapter.
The culaSparseFlag data type is an output enumeration containing a set of all possible convergence and non-convergence cases that can be returned by the iterative solver routines. Possible elements include:
| Flag Value | Meaning |
|---|---|
| culaSparseConvergedToRelative | The solver converged to the specified relative tolerance |
| culaSparseConvergedToAbsolute | The solver converged to the specified absolute tolerance |
| culaSparseDiverged | The solver diverged by exceeding the specified divergence tolerance |
| culaSparseMaxIterationsReached | Maximum iterations reached without convergence |
| culaSparseMaxTimeReached | Maximum execution time reached without convergence |
| culaSparseStagnation | The solver stagnated |
| culaSparseBreakdown | An intermediate scalar value was out of range |
| culaSparseInterrupted | The routine was manually interrupted |
| culaSparseSolveNotExecuted | The solver was not executed |
| culaSparseUnknownIterationError | An unknown iteration error was encountered |
For more information about various failure status conditions, see the Common Errors chapter.
The culaIterativeConfig data type is an input structure that contains information that steers execution of iterative functions with the following fields:
| Name | Type | Description |
|---|---|---|
| relativeTolerance | double | The relative tolerance for which convergence is achieved. |
| absoluteTolerance | double | The absolute tolerance for which convergence is achieved. |
| diverganceTolerance | double | The relative tolerance of the residual norm for which the iterative solver will determine the server is diverging. |
| maxIterations | int | The maximum number of iterations that the solver will attempt. |
| maxRuntime | int | The maximum time, in seconds, at which the solver will not begin a new iteration. If set to 0, the solver will run until convergence or the maximum number of iterations has been reached. |
| residualVector | double* | This parameter provides the means for a user to capture the residual at each iteration. The specified array must be at least maxIter in length. This parameter may be NULL if these quantities are not desired. |
| useInitialResultVector | int | Indicates whether the ‘x’ vector in iterative solves should be used as given or ignored. When ignored, the ‘x’ vector is considered a zero. |
| useBestAnswer | int | Indicates whether the ‘x’ vector in iterative solves should return the final answer or the best answer and its associated iteration number in the case of non-convergence. |
| useStagnationCheck | int | Indicates whether to check whether the iterative solve stagnated. This option defaults to on; turning this option off will increase performance if a problem is certain not to stagnate. |
The culaIterativeResidual data type is an output structure that contains information about the residual of an iterative function with the following fields:
| Member | Type | Description |
|---|---|---|
| r0 | double | The norm of the initial preconditioned residual vector |
| relative | double | The relative residual obtained by the solver |
| absolute | double | The absolute residual obtained by the solver |
| byIteration | double* | If requested, the residual at every step of iteration |
For more information, see Residual Vector.
The culaIterativeTiming data type is an output structure containing timing information for execution of an iterative function with the following fields:
| Member | Type | Description |
|---|---|---|
| solve | double | Time, in seconds, the solve portion of the iterative solver took to complete |
| preconditioner | double | Time, in seconds, the preconditioner generative portion of the iterative solver took to complete |
| overhead | double | Time, in seconds, of overhead needed by the iterative solver; includes memory transfers to-and-from the GPU |
| total | double | Time, in seconds, the entire iterative solver took to complete |
For more information see Timing Results.
The culaSparseResult data type is an output structure containing information regarding the execution of the iterative solver and associated preconditioner. Fields in this data type include:
| Name | Type | Description |
|---|---|---|
| config | culaSparseConfig | Copy of the configuration a given solver was called with |
| flag | culaSparseFlag | Enumeration containing information about the success or failure of the iterative solver |
| iterations | int | Number of iterations taken by the iterative solver |
| residual | culaSparseResidualInfo | Structure containing information about the residual |
| timing | culaSparseTiming | Structure containing timing information about the iterative solver and associated preconditioners |
| code | unsigned int | Internal information code |
The culaSparseReordering data type is an enum that specifies a reordering strategy for the input data. For some matrices, reordering can introduce additional parallelism that can allow the solver or preconditioner to execute more efficiently on a parallel device.
| Reordering Value | Meaning |
|---|---|
| culaSparseNoReordering | Do not do any reordering |
| culaSparseAmdReordering | Reorder using the approximate minimum degree ordering method |
| culaSparseSymamdReordering | Reorder using the symmetric minimum degree ordering method (SYMAMD) |
Reordering can be expensive in terms of additional memory required. COLAMD requires approximately \(2.2 * NNZ + 7 * N + 4 * M\) extra elements of storage.
The culaSparseSparsityPattern data type is an enum that specifies a sparsity pattern for some routines.
| Sparsity Pattern Value | Meaning |
|---|---|
| culaSparseAPattern | Uses the same sparsity pattern as A |
| culaSparseA2Pattern | Uses a sparsity pattern of A^2 |
| culaSparseA3Pattern | Uses a sparsity pattern of A^3 |
| culaSparseA4Pattern | Uses a sparsity pattern of A^4 |
Pattern generation can be expensive if the resulting pattern has a large number of values.
Platform, solver, and preconditioner options structures allow you to steer the execution of a given platform, solver, and preconditioner. For documentation on individual options structures, see the corresponding solver or preconditioner section.
Initializing these structures is done with a method that matches the name of the associated solver or preconditioner with an Init appended.
// create options structure
culaSparseBicgOptions solverOpts;
// initialize values
culaSparseBicgOptionsInit(handle, &solverOpts);
// configure specific parameters (if applicable)
// ...
Several options structures have reserved parameters. These structures are implemented in this way so as to maintain uniformity in the solver parameter list and to provide compatibility for possible future code changes. We recommend that you make sure to call the options initialization function (as shown above) for all options in the case that any parameters are added to it in the future. For routines that take an option structure, a NULL pointer may be passed, in which case reasonable defaults will be assigned.
CULA Sparse supports a number of processing platforms with different performance and data locality charactertics. Using the plan interface, this preference is set using a function call. These routines take a platform option parameter specific to the platform and have the form of culaSparseSet{Platform}(...) where the value enclosed by :c:type`{Platform}`s are one of the values outlined below.
| Platform | Description |
|---|---|
| Host | Use the multi-core host platform (host pointers) |
| Cuda | Use the CUDA-accelerated GPU platform (host pointers) |
| CudaDavice | Use the CUDA-accelerated GPU platform (CUDA pointers) |
This platform uses the system’s multi-core process for execution.
#include <cula_sparse.h>
// initialize host platform options
culaSparseHostOptions platformOpts;
culaSparseStatus status = culaSparseHostOptionsInit(handle, &precondOpts);
// set host platform
status = culaSparseSetHostPlatform(handle, &platformOpts);
| Name | Type | Description |
|---|---|---|
| indexing | int | Indicates whether the sparse indexing arrays are represented using 0 (C/C++) or 1 (FORTRAN) based indexing. |
| reordering | culaSparseReordering | Selects a reordering method to apply to the input matrix prior to any processing. This operation is applied to a copy of the matrix rather than actual input data. |
| debug | int | Specifies whether to perform extra checks to aid in debugging. |
This platform uses the NVIDIA CUDA platform for accelerated execution. All matrix and vector pointers reference by the data format objects are allocated on the host.
#include <cula_sparse.h>
// initialize CUDA platform options
culaSparseCudaOptions platformOpts;
culaSparseStatus status = culaSparseCudaOptionsInit(handle, &precondOpts);
// set CUDA platform
status = culaSparseSetCudaPlatform(handle, &platformOpts);
| Name | Type | Description |
|---|---|---|
| reordering | culaSparseReordering | Selects a reordering method to apply to the input matrix prior to any processing. This operation is applied to a copy of the matrix rather than actual input data. |
| deviceId | int | Select the CUDA device for which all operations will take place. The device identifiers are enumerated by the CUDA API. |
| useHybridFormat | int | Optionally use the hybrid matrix optimization which may result in higher performance for many matrix structures at the expense of higher memory usage. |
| debug | int | Specifies whether to perform extra checks to aid in debugging. |
This platform uses the NVIDIA CUDA platform for accelerated execution. All matrix and vector pointers reference by the data format objects are allocated on the CUDA device.
#include <cula_sparse.h>
// initialize CUDA Device platform options
culaSparseCudaDeviceOptions platformOpts;
culaSparseStatus status = culaSparseCudaDeviceOptionsInit(handle, &precondOpts);
// set CUDA Device platform
status = culaSparseSetCudaDevicePlatform(handle, &platformOpts);
| Name | Type | Description |
|---|---|---|
| reordering | culaSparseReordering | Selects a reordering method to apply to the input matrix prior to any processing. This operation is applied to a copy of the matrix rather than actual input data. |
| deviceId | int | Select the CUDA device for which all operations will take place. The device identifiers are enumerated by the CUDA API. The device id must be the same as where memory allocation took place using cudaMalloc. |
| useHybridFormat | int | Optionally use the hybrid matrix optimization which may result in higher performance for many matrix structures at the expense of higher memory usage. |
| debug | int | Specifies whether to perform extra checks to aid in debugging. |
This data format uses the compressed sparse row data format.
#include <cula_sparse.h>
culaSparseScsrDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCsrOptions* platformOpts, const float* a, const int* rowPtr, const int* colInd, float* x, cosnt float* b);
culaSparseDcsrDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCsrOptions* platformOpts, const double* a, const int* rowPtr, const int* colInd, double* x, cosnt double* b);
culaSparseCcsrDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCsrOptions* platformOpts, const culaSparseComplexFloat* a, const int* rowPtr, const int* colInd, culaSparseComplexFloat* x, cosnt culaSparseComplexFloat* b);
culaSparseZcsrDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCsrOptions* platformOpts, const culaSparseComplexDouble* a, const int* rowPtr, const int* colInd, culaSparseComplexDouble* x, cosnt culaSparseComplexDouble* b);
| Name | Type | Description |
|---|---|---|
| indexing | int | 0 or 1 based offset of the index values |
For more information about storage format specifics, see Sparse Matrix Storage Formats.
This data format uses the sparse coordinate row data format.
#include <cula_sparse.h>
culaSparseScooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCooOptions* platformOpts, const float* a, const int* rowInd, const int* colInd, float* x, cosnt float* b);
culaSparseDcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCooOptions* platformOpts, const double* a, const int* rowInd, const int* colInd, double* x, cosnt double* b);
culaSparseCcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCooOptions* platformOpts, const culaSparseComplexFloat* a, const int* rowInd, const int* colInd, culaSparseComplexFloat* x, cosnt culaSparseComplexFloat* b);
culaSparseZcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCooOptions* platformOpts, const culaSparseComplexDouble* a, const int* rowInd, const int* colInd, culaSparseComplexDouble* x, cosnt culaSparseComplexDouble* b);
| Name | Type | Description |
|---|---|---|
| indexing | int | 0 or 1 based offset of the index values |
For more information about storage format specifics, see Sparse Matrix Storage Formats.
This data format uses the compressed sparse column row data format.
#include <cula_sparse.h>
culaSparseScooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCscOptions* platformOpts, const float* a, const int* rowInd, const int* colPtr, float* x, cosnt float* b);
culaSparseDcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCscOptions* platformOpts, const double* a, const int* rowInd, const int* colPtr, double* x, cosnt double* b);
culaSparseCcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCscOptions* platformOpts, const culaSparseComplexFloat* a, const int* rowInd, const int* colPtr, culaSparseComplexFloat* x, cosnt culaSparseComplexFloat* b);
culaSparseZcooDataFormat(culaSparseHandle handle, culaSparsePlan plan, const culaSparseCscOptions* platformOpts, const culaSparseComplexDouble* a, const int* rowInd, const int* colPtr, culaSparseComplexDouble* x, cosnt culaSparseComplexDouble* b);
| Name | Type | Description |
|---|---|---|
| indexing | int | 0 or 1 based offset of the index values |
For more information about storage format specifics, see Sparse Matrix Storage Formats.
This data format utilizes a user supplied function that returns \(x' = A*x\) or \(x' = A^t*x\) opposed to explicitly performing the multiplication. This is achieved through a C function pointer that is called whenever an iterative solver needs to perform matrix-vector multiplication. As described in the following table, the function pointer must accept a transpose character, a constant input vector, an output vector, and a void pointer that may contain user data (the parameter names provided in the function pointer are just suggestions and don’t have to match the user provided function).
This data format is not available in the legacy interface.
| Name | Type | Description |
|---|---|---|
| trans | char | ‘N’ for transpose; ‘T’ for transpose; ‘C’ for conjugate transpose (current only the BiCG solver will require a transpose) |
| input | const data* | typed-pointer to the input vector of x |
| output | data* | typed-pointer to the output vector that should contain Ax after the function call |
| user | void* | pass-through of the void pointer passed into the format creation; useful for transporting user defined data |
#include <cula_sparse.h>
struct user_t { ... };
void ax(char trans, const double* input, double* output, void* user)
{
// user parameters
user_t user_parameters = (user_t*)(user);
// perform operation
// trans == 'N' : output = A * input
// trans == 'T' : output = A^T * input (transpose)
// trans == 'C' : output = A^H * input (conjugate transpose)
}
user_t user;
culaSparseSetDmatrixfreeData(handle, plan, platformOpts, n, ax, &user, x, b);
When using the host platform, the data pointers point to host allocated memory. On the CUDA and CUDA Device platforms, the data pointers point to CUDA allocated memory.
| Name | Type | Description |
|---|---|---|
| reserved | int | reserved |
Preconditioning is an additional step to aid in convergence of an iterative solver. This step is simply a means of transforming the original linear system into one which has the same solution, but which is most likely easier to solve with an iterative solver. Generally speaking, the inclusion of a preconditioner will decrease the number of iterations needed to converge upon a solution. Proper preconditioner selection is necessary for minimizing the number of iterations required to reach a solution. However, the preconditioning step does add additional work to every iteration as well as up-front processing time and additional memory. In some cases this additional work may end up being a new bottleneck and improved overall performance may be obtained using a preconditioner that takes more steps to converge, but the overall runtime is actually lower. As such, we recommend analyzing multiple preconditioner methods and looking at the total runtime as well the number of iterations required.
This chapter describes several preconditioners, which have different parameters in terms of effectiveness, memory usage, and setup/apply time.
For additional algorithmic details regarding the methods detailed in this chapter, we recommend reading the “Preconditioning Techniques” chapter from Yousef Saad’s textbook “Iterative Methods for Sparse Linear Systems”.
To solve a system without a preconditioner, simply do not associate the plan with a preconditioner. To remove a previously associated preconditioner call the culaSparseNoPreconditioner routine.
#include <cula_sparse.h>
// initialize cg options
culaSparseEmptyOptions precondOpts;
culaSparseStatus status = culaSparseEmptyOptionsInit(handle, &precondOpts);
// associate plan with no preconditioner
status = culaSparseSetNoPreconditioner(handle, plan, &solverOpts);
The Jacobi precondition is a simple preconditioner that is a replication of the diagonal:
The Jacobi preconditioner is very lightweight in generation, memory usage, and application. As such, it is often a strong choice for GPU accelerated solvers.
The Jacobi preconditioner is associated with a plan by calling the culaSparseSetJacobiPreconditioner with the culaSparseJacobiOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize jacobi options
culaSparseJacobiOptions precondOpts;
culaSparseStatus status = culaSparseJacobiOptionsInit(handle, &precondOpts);
// associate plan with jacobi preconditioner
status = culaSparseSetJacobiPreconditioner(handle, plan, &solverOpts);
The Block Jacobi preconditioner is an extension of the Jacobi preconditioner where the matrix is now represented as a block diagonal of size \(b\):
This preconditioner is a natural fit for systems with multiple physical variables that have been grouped into blocks.
The Block Jacobi preconditioner requires more computation in both generation and application than the simpler Jacobi preconditioner. However, both generation and application are parallel operations that map well to the GPU.
The Block Jacobi preconditioner is associated with a plan by calling the culaSparseSetBlockPreconditioner with the culaSparseBlockJacobiOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize cg options
culaSparseBlockjacobiOptions precondOpts;
culaSparseStatus status = culaSparseBlockjacobiOptionsInit(handle, &precondOpts);
// associate plan with block jacobi preconditioner
status = culaSparseSetBlockjacobiPreconditioner(handle, plan, &solverOpts);
| Name | Type | Description |
|---|---|---|
| blockSize | int | Block size for the Jacobi Preconditioner |
The ILU0 preconditioner is an incomplete LU factorization with zero fill-in, where \(L*U \approx A\):
The ILU0 preconditioner is lightweight in generation, and due to the zero-fill component, requires roughly the same memory as the linear system trying to be solved. In application, the ILU0 preconditioner requires two triangular solve routines - a method not well suited for parallel processing platforms such as the GPU or multicore processors. As such, using the ILU0 preconditioner may result in a reduced number of iterations at the cost of a longer runtime.
In comparison to Jacobi, the construction and application time and the memory requirements are higher for ILU0. For some matrices, the ILU0 might result in significantly improved convergence, which can offset the costs.
In order to successfully complete the factorization, the input matrix must have a diagonal entry in every row, and it must be nonzero. Failure to meet this criteria will result in a culaSparsePreconditionerError code.
The ILU0 preconditioner is associated with a plan by calling the culaSparseSetIlu0Preconditioner with the culaSparseIlu0Options input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize cg options
culaSparseIlu0Options precondOpts;
culaSparseStatus status = culaSparseIlu0OptionsInit(handle, &precondOpts);
// associate plan with ilu0 preconditioner
status = culaSparseSetIlu0Precondition(handle, plan, &solverOpts);
The factorized approximate inverse preconditioner is an incomplete approximation of the inverse of a symmetric positive definite input matrix, where \(A*M \approx I\) and \(M\) has a sparsity pattern as specified by culaSparseSparsityPattern. Fundamentally, the preconditioner attempts to minimize the Frobenius norm:
The approximate inverse preconditioner is heavyweight in generation. However, the algorithm expresses per-column parallelism and therefor can be generated efficiently. Unlike ilu based preconditioners, this preconditioner is applied using matrix-vector multiplication which can reach very high performance on GPU based systems.
The approximate inverse preconditioner is associated with a plan by calling the culaSparseSetAinvPreconditioner function with the culaSparseAinvOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize ainv options
culaSparseAinvOptions precondOpts;
culaSparseStatus status = culaSparseAinvOptionsInit(handle, &precondOpts);
// associate plan with ainv preconditioner
status = culaSparseSetAinvPrecondition(handle, plan, &solverOpts);
| Name | Type | Meaning |
|---|---|---|
| pattern | culaSparseSparsityPattern | pattern of the generated preconditioner; defaults to match the input matrix |
| dropTolerance | double | absolute threshold for which small values are dropped from the preconditioner; this can help remove insignificantly small values from the preconditioner and therefor speed up application; set to zero for no dropping |
The approximate inverse preconditioner is an incomplete approximation of the inverse of the input matrix, where \(M = LL^T \approx I\) and \(M\) has a sparsity pattern as specified by culaSparseSparsityPattern. Fundamentally, the preconditioner attempts to minimize the Frobenius norm:
Unlike the standard approximate inverse preconditioner, this method generates a symmetric positive definite preconditioner appropriate for use with the conjugate gradient solver.
The factorized approximate inverse preconditioner is fairly heavyweight in generation. However, the algorithm expresses per-column parallelism and therefor can be generated efficiently. Unlike ilu based preconditioners, this preconditioner is applied using matrix-vector multiplication which can reach very high performance on GPU based systems.
The approximate inverse preconditioner is associated with a plan by calling the culaSparseSetAinvPreconditioner function with the culaSparseAinvOptions input struct parameter (see Options Structures).
The factorized approximate inverse preconditioner is associated with a plan by calling the culaSparseSetFainvPreconditioner function with the culaSparseFainvOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize fainv options
culaSparseFainvOptions precondOpts;
culaSparseStatus status = culaSparseFainv0OptionsInit(handle, &precondOpts);
// associate plan with fainv preconditioner
status = culaSparseSetFainvPrecondition(handle, plan, &solverOpts);
| Name | Type | Meaning |
|---|---|---|
| pattern | culaSparseSparsityPattern | pattern of the generated preconditioner; defaults to match the input matrix |
| dropTolerance | double | absolute threshold for which small values are dropped from the preconditioner; this can help remove insignificantly small values from the preconditioner and therefor speed up application; set to zero for no dropping |
The user defined preconditioner allows the user to provide a callback function to preconditioner an input vector such that \(z' = M^-1*z\).
This is achieved through a C function pointer that is called whenever an iterative solver needs to apply the preconditioner. As described in the following table, the function pointer must accept a transpose character, a constant input vector, an output vector, and a void pointer that may contain user data (the parameter names provided in the function pointer are just suggestions and don’t have to match the user provided function).
| Name | Type | Description |
|---|---|---|
| trans | char | ‘N’ for transpose; ‘T’ for transpose; ‘C’ for conjugate transpose (current only the BiCG solver will require a transpose) |
| input | const data* | typed-pointer to the input vector of z |
| output | data* | typed-pointer to the output vector that should contain \(M^1*z\) after the function call |
| user | void* | pass-through of the void pointer passed into the format creation; useful for transporting user defined data |
When using the host platform, the data pointers point to host allocated memory. On the CUDA and CUDA Device platforms, the data pointers point to CUDA allocated memory.
| Name | Type | Meaning |
|---|---|---|
| sApply | function pointer | call-back function to apply the single precision preconditioner |
| dApply | function pointer | call-back function to apply the double precision preconditioner |
| cApply | function pointer | call-back function to apply the single precision complex preconditioner |
| zApply | function pointer | call-back function to apply the double precision complex preconditioner |
This section describes the iterative solvers routines available in the CULA Sparse library.
For algorithmic details regarding the methods detailed in this chapter, we recommend reading the “Krylov Subspace Methods: Part 1 & 2” chapters from Yousef Saad’s textbook “Iterative Methods for Sparse Linear Systems”.
This family of functions attempt to solve \(Ax=b\) using the conjugate gradient (CG) method where \(A\) is a symmetric positive definite matrix stored in a sparse matrix format and \(x\) and \(b\) are dense vectors. The matrix must be a fully populated symmetric; i.e. for each populated entry \(A_{ij}\) there must be an identical entry \(A_{ji}\).
| Solver Trait | Value |
|---|---|
| matrix class | Symmetric Positive Definite |
| memory overhead | \(6n\) |
The conjugate gradient solver is associated with a plan by calling the culaSparseSetCgSolver with the culaSparseCgOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize cg options
culaSparseCgOptions solverOpts;
culaSparseStatus status = culaSparseCgOptionsInit(handle, &solverOpts);
// associate plan with cg solver
status = culaSparseSetCgSolver(handle, plan, &solverOpts);
| Name | In/out | Meaning |
|---|---|---|
| reserved | in | reserved for future compatibility |
This family of functions attempt to solve \(Ax=b\) using the conjugate gradient (BiCG) method where \(A\) is a square matrix stored in a sparse matrix format format and \(x\) and \(b\) are dense vectors. While BiCG may converge for general matrices, it is mathematically most suitable for symmetric systems that are not positive definite. For symmetric positive definite systems, this method is identical to but considerably more expensive than CG.
The biconjugate gradient solver is associated with a plan by calling the culaSparseSetBicgSolver with the culaSparseBicgOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize bicg options
culaSparseBicgOptions solverOpts;
culaSparseStatus status = culaSparseBicgOptionsInit(handle, &solverOpts);
// associate plan with bicg solver
status = culaSparseSetBicgSolver(handle, plan, &solverOpts);
| Name | In/out | Meaning |
|---|---|---|
| avoidTranspose | host | in Avoids repeated transpose operations by creating a transposed copy of the input matrix. May lead to improved speeds and accuracy at the expense of memory and computational overheads. |
This family of functions attempt to solve \(Ax=b\) using the conjugate gradient stabilized (BiCGSTAB) method where \(A\) is a square matrix stored in a sparse matrix format format and \(x\) and \(b\) are dense vectors. This method was developed to solve non-symmetric linear systems while avoiding the irregular convergence patterns of the Conjugate Gradient Squared (CGS) method.
| Solver Trait | Value |
|---|---|
| matrix class | General |
| memory overhead | \(10n\) |
The biconjugate gradient stabilized solver is associated with a plan by calling the culaSparseSetBicgstabSolver with the culaSparseBicgstabOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize bicgstab options
culaSparseBicgstabOptions solverOpts;
culaSparseStatus status = culaSparseBicgstabOptionsInit(handle, &solverOpts);
// associate plan with bicgstab solver
status = culaSparseSetBicgstabSolver(handle, plan, &solverOpts);
| Name | Memory | In/out | Meaning |
|---|---|---|---|
| reserved | host | in | reserved for future compatibility |
This family of functions attempt to solve \(Ax=b\) using the conjugate gradient stabilized (BiCGSTAB(L)) method where \(A\) is a square matrix stored in a sparse matrix format format and \(x\) and \(b\) are dense vectors. This method extendeds the BiCG algorithm by adding an additional GMRES step with a restart value of L after each BiCGSTAB iteration. In practice, this may help to smooth convergence - especially in cases where \(A\) has large complex eigenpairs.
| Solver Trait | Value |
|---|---|
| matrix class | General |
| memory overhead | \(n*L + 8n\) |
The biconjugate gradient stabilized (L) solver is associated with a plan by calling the culaSparseSetBicgstablSolver with the culaSparseBicgstablOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize bicgstabl options
culaSparseBicgstablOptions solverOpts;
culaSparseStatus status = culaSparseBicgstablOptionsInit(handle, &solverOpts);
// associate plan with bicgstabl solver
status = culaSparseSetBicgstablSolver(handle, plan, &solverOpts);
| Name | Memory | In/out | Meaning |
|---|---|---|---|
| l | host | in | restart value of the GMRES portion of the algorithm; directly related to memory useage |
This family of functions attempt to solve \(Ax=b\) using the restarted general minimal residual GMRES(m) method where \(A\) is a square matrix stored in a sparse matrix format and \(x\) and \(b\) are dense vectors. This method is implemented using the modified Gram-Schmidt method for orthogonalization. When a preconditioner is specified, GMRES attempts to minimize \(||Mb-MAx||/||b||\) opposed to \(||b-Ax||/||b||\) in the absence of a preconditioner.
The maximum iterations, specified by culaIterativeConfig, are in reference to the outer iteration count. The maximum inner iteration count is specified by the restart value contained in the culaGmresOptions parameter.
The gmres solver is associated with a plan by calling the culaSparseSetGmresSolver with the culaSparseGmresOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize gmres options
culaSparseGmresOptions solverOpts;
culaSparseStatus status = culaSparseGmresOptionsInit(handle, &solverOpts);
solverOpts.restart = 20;
// associate plan with gmres solver
status = culaSparseSetGmresSolver(handle, plan, &solverOpts);
| Solver Trait | Value |
|---|---|
| matrix class | General |
| memory overhead | \(n*m + 5n\) |
Note that the total memory overhead is directly proportional to the restart value, and so care should be taken with this parameter.
This family of functions attempt to solve \(Ax=b\) using the minimum residual method MINRES method where \(A\) is a square matrix stored in a sparse matrix format and \(x\) and \(b\) are dense vectors. When a preconditioner is specified, MINRES attempts to minimize \(||Mb-MAx||/||b||\) opposed to \(||b-Ax||/||b||\) in the absence of a preconditioner.
| Solver Trait | Value |
|---|---|
| matrix class | General |
| memory overhead | \(11n\) |
The minres solver is associated with a plan by calling the culaSparseSetMinresSolver with the culaSparseMinresOptions input struct parameter (see Options Structures).
#include <cula_sparse.h>
// initialize minres options
culaSparseMinresOptions solverOpts;
culaSparseStatus status = culaSparseMinresOptionsInit(handle, &solverOpts);
// associate plan with minres solver
status = culaSparseSetMinresSolver(handle, plan, &solverOpts);
| Name | In/out | Meaning |
|---|---|---|
| restart | in | number of inner iterations at which point the algorithm restarts; directly related to memory usage |
This chapter describes the Legacy Interface found in cula_sparse_legacy.h():
The legacy interface provides a single function call interface to achieve all of the capability of the standard interface. Due to the number of platforms, data formats, solvers, and preconditioenrs, the combinatorial number of functions in this interface is very large. Five major concepts are conveyed by the function names of the iterative system solvers:
#include <cula_sparse_legacy.h>
culaSparse{platform}{type}{storage}{solver}{precond}(...)
Here, each {...} segment represents a different major component of the routine. The following table explains each of these components:
| Name | Meaning |
|---|---|
| platform | execution platform |
| type | data type used |
| storage | sparse matrix storage format used |
| solvers | iterative method used |
| precond | preconditioner method used |
For example, the routine culaSparseCudaDcsrCgJacobi() will use the CUDA platform to attempt to solve a double precision sparse matrix stored in the compressed sparse row (CSR) storage format using the conjugate gradient (CG) method with Jacobi preconditioning.
This chapter outlines the auxiliary functions available in the CULA Sparse library.
| Function | Purpose |
|---|---|
| culaSparsePreinitializeCuda | A standalone function to initialize the CUDA runtime rather than during the first function call |
| culaSparseGetConfigString | Returns a printable string with information regarding the configuration structure |
| culaSparseGetLastStatusString | Returns a printable string with additional information regarding the previous status associated with the handle |
| culaSparseGetResultString | Returns a printable string with information regarding the result structure |
This chapter outlines many of the performance and accuracy considerations pertaining to the CULA Sparse library. There are details regarding how to get the most performance out of your solvers and provide possible reasons why a particular solver may be under performing.
Many of the solvers in CULA Sparse library should use the double precision data format to achieve convergence in less iterations. While users of the NVIDIA GeForce line may still see an appreciable speedup, we recommend using the NVIDIA Tesla line of compute cards with greatly improved double precision performance.
The modern GPU is optimized to handle large, massively parallel problems with a high computation to memory access ratio. As such, small problems with minimal parallelism will perform poorly on the GPU and are much better suited for the CPU where they can reside in cache memory. Typical problem sizes worth GPU-acceleration are systems with at least 10,000 unknowns and at least 30,000 non-zero elements.
For storage and performance reasons, the compressed sparse row (CSR) format is preferred as many internal operations have been optimized for this format. For other storage formats, CULA Sparse will invoke accelerated conversions routines to convert to CSR internally. To measure this conversion overhead, inspect the overhead field of the timing structure in the culaIterativeResult return structure. These conversion routines also require an internal buffer of size \(nnz\) which for large problems may be more memory than is available on the GPU.
Proper preconditioner selection is necessary for minimizing the number of iterations required to solve a solution. However, as mentioned in previous chapters, the preconditioning step does add additional work to every iteration. In some cases this additional work may end up being a new bottleneck and improved overall performance may be obtained using a preconditioner that takes more steps to converge, but the overall runtime is actually lower. As such, we recommend analyzing multiple preconditioner methods and looking at the total runtime as well the number of iterations required.
Iterative methods are typically very sensitive to numerical precision. Therefore, different implementations of the same algorithm may take a different number of iterations to converge to the same solution. This is as expected when dealing with the non-associative nature of floating point computations.
Unless otherwise specified, all of CULA Sparse’s iteration calculations are done with regards to a residual relative to the norm of the right hand side of the linear system. The defining equation for this is \(||b-Ax||/||b||\).
This section shows a very simple example of how to use the CULA Sparse API. Please note this example does no error checking and uses default parameters for each option. For a more complete example, see the iterativeSystemSolve SDK example.
#include <cula_sparse.h>
int main()
{
// test data
const int n = 8;
const int nnz = 8;
double a[nnz] = { 1., 2., 3., 4., 5., 6., 7., 8. };
double x[n] = { 1., 1., 1., 1., 1., 1., 1., 1. };
double b[n];
int colInd[nnz] = { 0, 1, 2, 3, 4, 5, 6, 7 };
int rowInd[nnz] = { 0, 1, 2, 3, 4, 5, 6, 7 };
// character buffer used for results and error messages
char buf[256];
// create library handle
culaSparseHandle handle;
culaSparseCreate(&handle);
// create execution plan
culaSparsePlan plan;
culaSparseCreatePlan(handle, &plan);
// use the CUDA platform
culaSparseCudaPlatform(handle, plan, 0)
// associate coo data with the plan
culaSparseSetDcooData(handle, plan, 0, n, nnz, a, rowInd, colInd, x, b);
// associate cg solver with the plan
culaSparseSetCgSolver(handle, plan, 0);
// associate jacobi preconditioner with the plan
culaSparseSetJacobiPreconditioner(handle, plan, 0);
// execute plan
culaSparseExecutePlan(handle, plan, &config, &result);
// cleanup
culaSparseDestroyPlan(plan);
culaSparseDestroy(handle);
}
This section describes how to set up CULA Sparse using common tools, such as Microsoft® Visual Studio®, as well as command line tools for Linux and Mac OS X.
This section describes how to configure Microsoft Visual Studio to use CULA Sparse. Before following the steps within this section, take note of where you installed CULA Sparse (the default is C:\Program Files\CULA\S#). To set up Visual Studio, you will need to set both Global- and Project-level settings. Each of these steps is described in the sections below.
When inside Visual Studio, navigate to the menu bar and select Tools > Options. A window will open that offers several options; in this window, navigate to Projects and Solutions > VC++ Directories. From this dialog you will be able to configure global executable, include, and library paths, which will allow any project that you create to use CULA Sparse.
The table below specifies the recommended settings for the various directories that the VC++ Directories dialog makes available. When setting up your environment, prepend the path of your CULA Sparse installation to each of the entries in the table below. For example, to set the include path for a typical installation, enter C:\Program Files\CULA\include for the Include Files field.
| Option | Win32 | x64 |
|---|---|---|
| Executable Files | bin | bin64 |
| Include Files | include | include |
| Library Files | lib | lib64 |
With these global settings complete, Visual Studio will be able to include CULA Sparse files in your application. Before you can compile and link an application that uses CULA Sparse, however, you will need to set up your project to link CULA Sparse.
To use CULA Sparse, you must instruct Visual Studio to link CULA Sparse to your application. To do this, right-click on your project and select Properties. From here, navigate to Configuration Properties > Linker > Input. In the Additional Dependencies field, enter “cula_core.lib cula_sparse.lib”.
On the Windows platform, CULA Sparse’s libraries are distributed as a dynamic link library (DLL) (cula_sparse.dll) and an import library (cula_sparse.lib), located in the bin and lib directories of the CULA Sparse installation, respectively. By Linking cula_sparse.lib, you are instructing Visual Studio to make an association between your application and the CULA Sparse DLL, which will allow your application to use the code that is contained within the CULA Sparse DLL.
CULA Sparse is built as a dynamically linked library, and as such it must be visible to your runtime system. This requires that cula_sparse.dll and its supporting dll’s are located in a directory that is a member of your system’s runtime path. On Windows, you may do one of several things:
- Add CULASPARSE_BIN_PATH_32 or CULASPARSE_BIN_PATH_64 to your PATH environment variable.
- Copy cula_sparse.dll and its supporting dll’s to the working directory or your project’s executable.
On a Linux system, a common way of building software is by using command line tools. This section describes how a project that is command line driven can be configured to use CULA Sparse.
The first step in this process is to set up environment variables so that your build scripts can infer the location of CULA Sparse.
On a Linux or Mac OS X system, a simple way to set up CULA Sparse to use environment variables. For example, on a system that uses the bourne (sh) or bash shells, add the following lines to an appropriate shell configuration file (e.g. .bashrc).
export CULASPARSE_ROOT=/usr/local/culasparse
export CULASPARSE_INC_PATH=$CULASPARSE_ROOT/include
export CULASPARSE_BIN_PATH_32=$CULASPARSE_ROOT/bin
export CULASPARSE_BIN_PATH_64=$CULASPARSE_ROOT/bin64
export CULASPARSE_LIB_PATH_32=$CULASPARSE_ROOT/lib
export CULASPARSE_LIB_PATH_64=$CULASPARSE_ROOT/lib64
(where CULASPARSE_ROOT is customized to the location you chose to install CULA Sparse)
After setting environment variables, you can now configure your build scripts to use CULA Sparse.
Note
You may need to reload your shell before you can use these variables.
This section describes how to set up the gcc compiler to include CULA Sparse in your application. When compiling an application, you will typically need to add the following arguments to your compiler’s argument list:
| Item | Command |
|---|---|
| Include Path | -I$CULASPARSE_INC_PATH |
| Library Path (32-bit arch) | -L$CULASPARSE_LIB_PATH_32 |
| Library Path (64-bit arch) | -L$CULASPARSE_LIB_PATH_64 |
| Libraries to Link against | -lcula_sparse |
For a 32-bit compile:
gcc ... -I$CULASPARSE_INC_PATH -L$CULASPARSE_LIB_PATH_32 ...
-lcula_sparse -lcublas -lcudart -lcusparse -liomp5 ...
For a 64-bit compile (not applicable to Mac OS X):
gcc ... -I$CULASPARSE_INC_PATH -L$CULASPARSE_LIB_PATH_64 ...
-lcula_sparse -lcublas -lcudart -lcusparse -liomp5 ...
CULA Sparse is built as a shared library, and as such it must be visible to your runtime system. This requires that CULA Sparse’s shared libraries are located in a directory that is a member of your system’s runtime library path. On Linux, you may do one of several things:
- Add CULASPARSE_LIB_PATH_32 or CULASPARSE_LIB_PATH_64 to your LD_LIBRARY_PATH environment variable.
- Edit your system’s ld.so.conf (found in /etc) to include either CULASPARSE_LIB_PATH_32 or CULASPARSE_LIB_PATH_64.
On the Mac OS X platform, you must edit the DYLD_LIBRARY_PATH environment variable for your shell, as above.
This chapter provides solutions to errors commonly encountered when using the CULA Sparse library.
As a general note, whenever an error is encountered, consider enabling debugging mode. The configuration parameter offers a debugging flag that, when set, causes CULA Sparse to perform many more checks than it would normally. These checks can be computationally expensive and so are not enabled on a default run. These checks may highlight the issue for you directly, saving you from having to do more time consuming debugging. Debugging output will occur as either a culaSparseStatus return code (i.e., a malformed matrix may be printed to the console, or returned via the result culaBadStorageFormat or via the result structure.
Problem
A function’s culaSparseStatus return code is equal to culaSparseArgumentError.
Description
This error indicates that one of your parameters to your function is in error. The culaSparseGetLastStatusString function will report which particular parameter is in error. Typical errors include invalid sizes or null pointers.
Solution
Check the noted parameter against the routine’s documentation to make sure the input is valid.
Problem
A function’s culaSparseStatus return code is equal to culaSparseDataFormatError.
Description
This error indicates that the set of inputs describing a sparse matrix is somehow malformed. If the debugging flag is set, the culaSparseGetLastStatusString function will report which particular parameter is in error. Typical errors include invalid sizes or null pointers.
There are many conditions which can trigger this, of which a few common examples are listed below.
There are many others, and the above may not be true for all matrix types.
Solution
Check the matrix data against the documentation for matrix storage types to ensure that it meets any necessary criteria.
Upon a culaSparseNonConvergence return code, it is possible to obtain more information by examining the culaSparseFlag within the culaSparseResult structure. This will indicate a problem with of the following errors:
Problem
A function’s culaSparseStatus return code is equal to culaSparseNonConvergence and the culaSparseFlag is indicating culaSparseMaxIterationsReached.
Description
This error indicates that the solver has reached a maximum number of iterations before the an answer within the given tolerance was reached.
Solution
Increase the iteration count or lower the desired tolerance. Also, the given solver and/or preconditioner might not be appropriate for your data. If this is the case, try a different solver and/or preconditioner. It is also possible that the input matrix may not be solvable with any of the methods available in CULA Sparse.
This might also be a desirable outcome in the case that the user is seeking the best possible answer within a budgeted number of iterations. In this case, the “error” can be safely ignored.
Problem
A function’s culaSparseStatus return code is equal to culaSparseNonConvergence and the culaSparseFlag is indicating culaSparseStagnation.
Description
The selected iterative solver has stagnated by calculating the same residual for multiple iterations in a row. The solver has exited early because a better solution cannot be calculated.
Solution
A different iterative solver and/or preconditioner may be necessary. It is also possible that the input matrix may not be solvable with any of the methods available in CULA Sparse.
It is implicit when this error is issued that the current residual still exceeds the specified tolerance, but the result may still be usable if the user is looking only for a “best effort” solution. In that case, this “error” can be disregarded.
Problem
A function’s culaSparseStatus return code is equal to culaSparseNonConvergence and the culaSparseFlag is indicating culaSparseBreakdown.
Description
The selected iterative solver has encountered an invalid floating point value during calculations. It is possible the method has broken down and isn’t able to solve the provided linear system.
Solution
Therefore, a different iterative solver and/or preconditioner may be necessary. It is also possible that the input matrix may not be solvable with any of the methods available in CULA Sparse. Also, it is possible the input matrix has improperly formed data.
Problem
A function’s culaSparseStatus return code is equal to culaSparseNonConvergence and the culaSparseFlag is indicating culaSparseUnknownIterationError.
Description
The selected iterative solver has encountered an unknown error.
Solution
This error is unexpected and should be reported the CULA Sparse development team.
Problem
A function’s culaSparseStatus return code is equal to culaSparsePreconditionerError.
Description
The preconditioner failed to generate and no iterations were attempted. This error is usually specific to different preconditioner methods but typically indicates that there is either bad data (i.e., malformed matrix) or a singular matrix. See the documentation for the preconditioner used, as it may specify certain conditions which must be met.
Solution
More information can be obtained through the culaSparseGetLastStatusString() function. In many cases the input matrix is singular and factorization methods such as ILU0 are not appropriate. In this case, try a different preconditioner and check that the structure of your matrix is correct.
Problem
A function’s culaSparseStatus return code is equal to culaSparseFeatureNotImplemented.
Description
Execution failed because a necessary internal function is not implemented.
Solution
More information can be obtained through the culaSparseGetLastStatusString() function. In some cases, certain preconditioner and solvers are only implemented for a specific platform or explicitly require a specific storage format.
Problem
A function’s culaSparseStatus return code is equal to culaSparseRuntimeError.
Description
An error associated with the selected platform’s runtime library has occurred. When using the CUDA platform, this error is commonly seen under a few circumstances:
- No capable GPU is found
- The CUDA GPU
- The installed CUDA driver is out-of-date
- Passing a device pointer into a function that is expected a host pointer or vise-versa
- The Window’s watchdog timer was exhausted
- Input data is malformed and out-of-bounds memory was accessed
Solution
More information can be obtained through the culaSparseGetLastStatusString() function. Check the common circumstances outlined above.
Problem
A function’s culaSparseStatus return code is equal to culaSparseAlignmentError.
Description
The CUDA Device platform requires data to be 16-byte aligned.
Solution
More information can be obtained through the culaSparseGetLastStatusString() function. Use the provided complex types to guarantee proper alignment.
Problem
A function’s culaSparseStatus return code is equal to culaSparseInsufficientMemory.
Description
Insufficient CPU or GPU memory was available to complete the requested operation. This includes storage for the input data, output data, and intermediates required by the solver.
Solution
Try another solver and/or preconditioner with a lower memory requirement. See each routine for details on how much memory is required to store the intermediate values.
If none of the entries in the Common Errors chapter solve your issue, you can seek technical support.
EM Photonics provides a user forum at http://www.culatools.com/forums at which you can seek help. Additionally, if your license level provides direct support, you may contact us directly.
When reporting a problem, make sure to include the following information:
- System Information
- CULA Version
- Version of NVIDIA® CUDA Toolkit installed, if any
- Problem Description (with code if applicable)
Occasionally you may need to send us your sparse matrix so that we can work with it directly. EM Photonics accepts two different sparse matrix formats:
- Matlab sparse matrices (.mat)
- Matrix-market format (.mtx)
Matlab’s sparse matrices are stored in .mat files. Matlab matrices can be saved with the ‘save’ command or by selecting a workspace variable and selecting ‘Save As’.
Matrix-market formats are discussed here: http://math.nist.gov/MatrixMarket/formats.html . This site contains routines for several languages for reading and writing to these file types.
For easy transfer to EM Photonics, please compress the matrix using one of .zip or .tar.gz compression methods.
Selecting the best sparse iterative solver and preconditioner is often a difficult decision. Very rarely can one simply know which combination will converge quickest to find a solution within the given constraints. Often the best answer requires knowledge pertaining to the structure of the matrix and the properties it exhibits. To help aid in the selection of a solver and preconditioner, we have constructed two flow charts to help gauge which solver and preconditioner might work best. Again, since there is no correct answer for any given system, we encourage users to experiment with different solvers, preconditioners, and options. These flowcharts are simply designed to give suggestions, and not absolute answers.
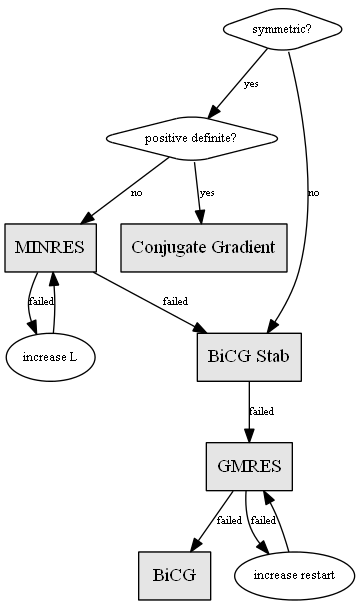
This flowchart assists in solver selection for your application.
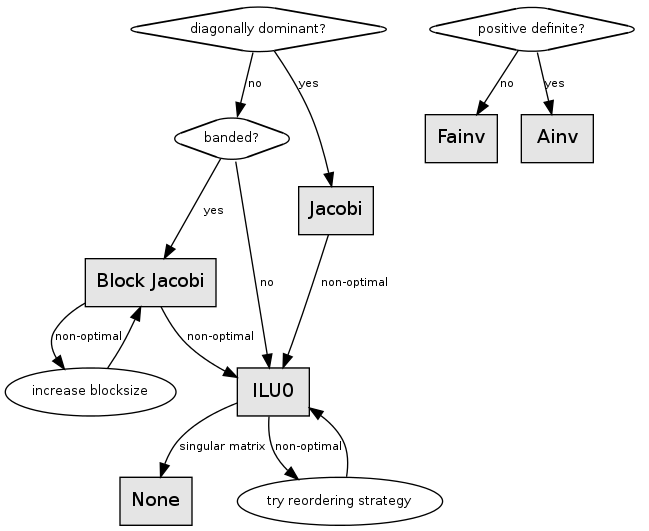
This flowchart assists in preconditioner selection for your application.